math assignment 4 class 9

Talk to our experts

1800-120-456-456

Important Questions for CBSE Class 9 Maths Chapter 4 - Linear Equations in Two Variables

• Class 9 Important Question
• Chapter 4: Linear Equations In Two Variables

Download Important Questions for Class 9 Maths Chapter 4 - Linear Equations in Two Variables - Free PDF

Vedantu has important questions for CBSE Class 9 Mathematics Chapter 4 - Linear Equations in Two Variables. These questions are developed in accordance with the most recent NCERT Curriculum Syllabus and are commonly asked in many sorts of examinations. These questions and answers will help students discover distinct patterns of conceptual issues that may appear on the final exam.

Download these Important Questions for Class 9 Maths Chapter 4 with Solutions PDF for free and use them to practice. Prepare the chapter well by using the solution format designed by the experts. You can also download NCERT Solutions for Class 9 Maths to help you to revise the complete syllabus and score more marks in your examinations. Students can also avail of NCERT Solutions Class 9 Science from our website. Besides, find CBSE Solutions to get more understanding of various subjects.

Download CBSE Class 9 Maths Important Questions 2024-25 PDF

Also, check CBSE Class 9 Maths Important Questions for other chapters:

Topics Covered in CBSE Class 9 Maths Chapter 4 - Linear Equations in Two Variables are as follows:

Linear Equations

Solution of a Linear Equation

Graph of a Linear Equation In Two Variables

Equations of Lines Parallel to the x-axis and y-axis

Important Questions from Linear Equations in Two Variables (Short, Long & Practice)

Short answer type questions.

1. Linear equation x – 2 = 0 is parallel to which axis?

2. If (1, -2) is a solution of the equation 2x – y = p, then find the value of p.

3. Express x/4 – 3y = – 7 in the form of ax + by + c = 0.

Long Answer Type Questions

1. If (2,3) and (4, 0) lie on the graph of equation ax + by = 1. Find the value of a and b. Plot the graph of the equation obtained.  

2. Draw the graphs of the following equations on the same graph sheet: x = 4,x = 2,y = l and y – 3 = 0

3. Represent 2x + 3y = 6 by a graph. Write the coordinates of the point where it meets: (a) x-axis (b) y-axis

Practice Questions

1. Find the two solutions of the linear equation 2x – 3y = 12.

2. Find the value of m if (5,8) is a solution of the equation 11 x-2y = 3m, then find one more solution of this equation.

3. On the graph paper draw the straight line 3x – 2y = 4 and x + y – 3 = 0. Also, find their point of intersection on the graph.

Class 9 Maths Chapter 4 Linear Equations in Two Variables Important Questions: Summary

As mentioned earlier, the 4 th chapter concentrates on the linear equations in two variables. The students will learn how an equation is formed using two variables and how they are solved. These new concepts will be used later in the advanced classes to understand the concepts of Cartesian coordinates and higher equations. To develop the concepts in this class even better, follow the Important Questions for Class 9 Maths Chapter 4 . The solutions are also provided for the questions.

These questions are prepared in accordance with the principles covered in the chapter. Students will learn how to employ these concepts in new and sophisticated ways by doing these questions. As a result, the primary goal of teachers is to demonstrate how formulae and concepts may be utilised to look forward and solve new issues. Teachers are aware of the kind of questions that will be asked on final examinations. Some will be simple, while others will be mentally hard. This is where solving Linear Equations in Two Variables Class 9 Crucial Questions will come in handy. Discover a few additional types of questions and how to answer them fast.

The 4 th chapter will teach how one variable is used to form an equation. It will also describe the different terms used in a linear equation. You will then proceed to learn how an equation is formed using two variables. Find out the difference between the linear equation of one variable and two variables. Check out Chapter 4 Maths Class 9 Important Questions to understand the new concepts even better.

How Can You Use Chapter 4 Maths Class 9 Important Questions?

Apart from studying the chapter and solving the exercise questions, adding these important questions for Class 9 Maths Chapter 4 to the study material is ideal. Let us check how you can use these questions for your betterment.

Solving Important Questions for Class 9 Maths Chapter 4 to Gain Another Perspective

The exercise-based questions are solved by all the students. What if you want to learn how different questions are formed for this chapter? This is where downloading these important questions can help you find out the different formats based on the same concepts taught in the chapter.

Answering these new questions will help you develop a new perspective to tackle the exam questions. You can use the solution provided to check how the teachers have formulated the approaches to solve these questions. Hence, your conceptual development will be a step ahead of the competition.

Easy Recapitulation of the Concepts

You can use the Class 9 Maths Chapter 4 Important Questions as a platform to recapitulate the new concepts you have learned in this chapter. Solving the same exercise questions might not give you the thrill. You will need the essence of these new questions to intellectually challenge your problem-solving skills. Find out your preparation level by answering these questions. You can also refer to the solution to learn how to solve these problems better.

Faster Completion of Preparation

How can you find out whether you are done with the preparation of a chapter? Use the Important Questions of Linear Equations in Two Variables Class 9 to find out whether you can solve them or not. If yes, then you are good to go. If not, then proceed to the solution section. Find out how the teachers have designed the solution and learn the chapter again efficiently.

Key Features of Important Questions CBSE Class 9 Maths Chapter 4 - Linear Equations in Two Variables

All the important questions are curated as per the exam point of view to help students score better.

Solutions are explained in a step-by-step manner for all questions.

All solutions are easy to understand and learn as they are clearly written by subject experts to match the curriculum.

These important questions help in developing a good conceptual foundation for students, which is important in the final stages of preparation for board and competitive exams.

These solutions are absolutely free and available in PDF format.

Key Concerns CBSE Class 9 Mathematics Chapter 4 Linear Equations in Two Variables is a valuable resource for students studying for the Class 9 Test. We have provided problems with solutions from highly significant areas covered by the NCERT Class 9 Linear Equations in Two Variables Syllabus. Students will also get an understanding of the kind of questions and methods used in the final test.

Important Related Links for CBSE Class 9 

Faqs on important questions for cbse class 9 maths chapter 4 - linear equations in two variables.

1. How can You Find More Questions Based on Linear Equations for Class 9?

The best way to find different kinds of questions is by downloading the Important Questions for Class 9 Maths Chapter 4 with Solutions. You will find a list of questions that can be used to prepare for new formats and challenges before an exam.

2. Why Should I Prefer Vedantu for Important Questions Related to Linear Equations of Class 9?

Vedantu is a one-stop online portal for Mathematics for Class 9 Students. They find quality NCERT solutions for Mathematics and sample papers to solve. They also find the Class 9 Maths Chapter 4 Important Questions to make their foundation of concepts better.

3. Are important questions of Chapter 4 of Class 9 Maths important from the exam point of view? 

Yes, important questions of Chapter 4 of Class 9 Maths are important from an exam point of view as these questions will help you save your time and get accurate answers to all the questions. You can prepare from these questions a day before your exam and cross-check all the solutions so as not to write wrong answers in your exams. The solutions are accurate, and you can rely on them to even understand the right method to solve your problems. The important questions are available free of cost on the Vedantu website and the Vedantu app.

4. Give me a summary of exercises present in Chapter 4 of Class 9 Maths.

It has the following topics; Introduction, Linear Equation, Solution Of Linear Equations, Graphs In Two Variables, Equations To Lines Parallel To X And Y-axis. Visit the official Vedantu website for additional details. There are important questions in this chapter that will assist you to pass your tests. These answers will cover all of the major themes that have been compiled from the exam's perspective. These questions are available for download and storage on your computer.

5. Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:

 x –(y/5)–10 = 0

This equation x –(y/5)-10 = 0 can also be written as 

Comparing 1x+(-⅕)y +(-10)=0 with ax+by+c=0

a= 1, b = -(⅕), c= -10

6. In the NCERT Solutions for Class 9 Maths linear equations in two variables, how many questions are there?

There are 16 questions in four exercises in NCERT Class 9 Maths Chapter 4 Linear Equations in Two Variables. All of these problems are paced in a way that allows students to gain a thorough understanding of linear equations, their solutions, and graphing. To arrange a time-based practise and preparation, divide these 16 questions into three categories: long replies, short level, and easy. NCERT Math solutions for Class 9 exercises on writing linear equations, finding solutions to linear equations, graphing linear equations, and graphical depiction of equations of lines parallel to the x and y axes are included in Chapter 4 linear equations in two variables.

7. Why must students build a strong foundation of Chapter 4 of Class 9 Maths?

The application of many algebraic ideas studied in higher grades requires the use of linear equations in two variables. Many real-life calculations, such as calculating profits, estimating values, and so on, are also vital to comprehend. As a result, students must have a solid foundation in this subject. The NCERT Solutions for Chapter 4 “Linear Equations in Two Variables” of Class 9 Maths carefully explain all of the key concepts so that students can easily absorb the knowledge.

CBSE Class 9 Maths Important Questions

Cbse study materials.

• CBSE Maths Important Questions
• Class 9 Maths
• Chapter 4: Linear Equations Two Variables

Important Questions CBSE Class 9 Maths Chapter 4-Linear Equation in Two Variables

Important Questions of CBSE Class 9 Maths Chapter 4 -Linear equations in two variables with solutions are available for the students who are preparing 9th final exam. These problems are solved by our experts, as per NCERT book formulated by CBSE board. It covers all the questions according to the syllabus, which is important as per the exam point of view.

Students can reach us at BYJU’S to get important questions for all chapter CBSE class 9 Maths . Practising these extra questions will also help them to revise all the concepts and get good marks in the examination.

Also Check:

• Important 2 Marks Questions for CBSE 9th Maths
• Important 3 Marks Questions for CBSE 9th Maths
• Important 4 Marks Questions for CBSE 9th Maths

Important Questions & Solutions For Class 9 Maths Chapter 4 (Linear Equation in Two Variables)

Q.1: Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:

(i) x – y/5 – 10 = 0

(ii) -2x+3y = 6

(iii) y – 2 = 0

(i) The equation x-y/5-10 = 0 can be written as:

(1)x + (-1/5) y + (-10) = 0

Now compare the above equation with ax + by + c = 0

Thus, we get;

(ii) –2x + 3y = 6

Re-arranging the given equation, we get,

–2x + 3y – 6 = 0

The equation –2x + 3y – 6 = 0 can be written as,

(–2)x + 3y +(– 6) = 0

Now comparing (–2)x + 3y +(– 6) = 0 with ax + by + c = 0

We get, a = –2

(iii) y – 2 = 0

The equation y – 2 = 0 can be written as,

0x + 1y + (–2) = 0

Now comparing 0x + 1y + (–2) = 0with ax + by + c = 0

We get, a = 0

Q.2. Write four solutions for each of the following equations:

(i) 2x + y = 7

To find the four solutions of 2x + y = 7 we substitute different values for x and y

(2×0)+y = 7

(2×1)+y = 7

The solutions are (0, 7), (1,5), (3,1), (2,3)

(ii) πx + y = 9

To find the four solutions of πx + y = 9 we substitute different values for x and y

(π × 0)+y = 9

(π×1)+y = 9

(π(-1))+y = 9

The solutions are (0,9), (1,9-π),(9/π,0),(-1,9+π)

Q.3: Find the value of k, if x = 2, y = 1 is a solution of the equation 2x + 3y = k.

The given equation is

2x + 3y = k

According to the question, x = 2 and y = 1.

Now, Substituting the values of x and y in the equation 2x + 3y = k,

⇒(2 x 2)+ (3 × 1) = k

The value of k, if x = 2, y = 1 is a solution of the equation 2x + 3y = k, is 7.

Q.4: Draw the graph of each of the following linear equations in two variables:

To draw a graph of linear equations in two variables, let us find out the points to plot.

To find out the points, we have to find the values for which x and y satisfies the given equation.

Substituting the values for x,

When x = 0,

When x = 1,

The points to be plotted are (0, 0) and (1, 3)

(ii) 3 = 2x + y

⇒ 3 = 2(0) + y

⇒ 3 = 0 + y

⇒ 3 = 2(1) + y

⇒ 3 = 2 + y

⇒ y = 3 – 2

The points to be plotted are (0, 3) and (1, 1)

Q.5: If the point (3, 4) lies on the graph of the equation 3y = ax + 7, find the value of a.

3y = ax + 7

According to the question, x = 3 and y = 4

Now, Substituting the values of x and y in the equation 3y = ax + 7,

(3×4) = (ax3) + 7

⇒ 12 = 3a+7

⇒ 3a = 12–7

The value of a, if the point (3, 4) lies on the graph of the equation 3y = ax + 7 is 5/3.

Q.6: Show that the points A (1, 2), B ( – 1, – 16) and C (0, – 7) lie on the graph of the linear equation y = 9x – 7.

We have the equation,

For A (1, 2),

Substituting (x,y) = (1, 2),

2 = 9(1) – 7

For B (–1, –16),

Substituting (x,y) = (–1, –16),

–16 = 9(–1) – 7

-16 = – 9 – 7

For C (0, –7),

Substituting (x,y) = (0, –7),

– 7 = 9(0) – 7

Hence, the points A (1, 2), B (–1, –16) and C (0, –7) satisfy the line y = 9x – 7.

Thus, A (1, 2), B (–1, –16) and C (0, –7) are solutions of the linear equation y = 9x – 7

Therefore, the points A (1, 2), B (–1, –16), C (0, –7) lie on the graph of linear equation y = 9x – 7.

Q.7: Draw the graph of the linear equation 3x + 4y = 6. At what points, the graph cuts X and Y-axis?

Solution: Given equation,

3x + 4y = 6.

We need at least 2 points on the graph to draw the graph of this equation,

Thus, the points the graph cuts

Since the point is on the x-axis, we have y = 0.

Substituting y = 0 in the equation, 3x + 4y = 6,

3x + 4×0 = 6

Hence, the point at which the graph cuts x-axis = (2, 0).

(ii) y-axis

Since the point is on the y-axis, we have, x = 0.

Substituting x = 0 in the equation, 3x + 4y = 6,

3×0 + 4y = 6

Hence, the point at which the graph cuts y-axis = (0, 1.5).

Plotting the points (0, 1.5) and (2, 0) on the graph.

​Extra Questions For Class 9 Maths Chapter 4

• The taxi fare in a city is as follows: For the first kilometre, the fare is ₹ 8 and for the subsequent distance it is ₹5 per km. Taking the distance covered as x km and total fare as ₹ y, write a linear equation for this information, and draw its graph.
• in one variable
• in two variables
• Write the linear equation such that each point on its graph has an ordinate 3 times its abscissa.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Hi, Please check this link: https://byjus.com/maths/important-questions-class-9-maths-chapter-4-linear-equations-two-variables/ . Thank you!

it was great

It was very helpful for me thankyou byjus .

It’s great

Thank You guys for posting these questions It is really helpful.

It is very useful while doing revision for exam. Thank you BYJU’S

Thank you for providing these question . It’s very useful while doing revisions in exam time

Thank you so much byjus for posting this questions. It was really helpful .

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

CBSE NCERT Solutions

NCERT and CBSE Solutions for free

Class 9 Mathematics Assignments

We have provided below free printable Class 9 Mathematics Assignments for Download in PDF. The Assignments have been designed based on the latest NCERT Book for Class 9 Mathematics . These Assignments for Grade 9 Mathematics cover all important topics which can come in your standard 9 tests and examinations. Free printable Assignments for CBSE Class 9 Mathematics , school and class assignments, and practice test papers have been designed by our highly experienced class 9 faculty. You can free download CBSE NCERT printable Assignments for Mathematics Class 9 with solutions and answers. All Assignments and test sheets have been prepared by expert teachers as per the latest Syllabus in Mathematics Class 9. Students can click on the links below and download all Pdf Assignments for Mathematics class 9 for free. All latest Kendriya Vidyalaya Class 9 Mathematics Assignments with Answers and test papers are given below.

Mathematics Class 9 Assignments Pdf Download

We have provided below the biggest collection of free CBSE NCERT KVS Assignments for Class 9 Mathematics . Students and teachers can download and save all free Mathematics assignments in Pdf for grade 9th. Our expert faculty have covered Class 9 important questions and answers for Mathematics as per the latest syllabus for the current academic year. All test papers and question banks for Class 9 Mathematics and CBSE Assignments for Mathematics Class 9 will be really helpful for standard 9th students to prepare for the class tests and school examinations. Class 9th students can easily free download in Pdf all printable practice worksheets given below.

Topicwise Assignments for Class 9 Mathematics Download in Pdf

More assignments for class 9 mathematics.

Advantages of Class 9 Mathematics Assignments

• As we have the best and largest collection of Mathematics assignments for Grade 9, you will be able to easily get full list of solved important questions which can come in your examinations.
• Students will be able to go through all important and critical topics given in your CBSE Mathematics textbooks for Class 9 .
• All Mathematics assignments for Class 9 have been designed with answers. Students should solve them yourself and then compare with the solutions provided by us.
• Class 9 Students studying in per CBSE, NCERT and KVS schools will be able to free download all Mathematics chapter wise worksheets and assignments for free in Pdf
• Class 9 Mathematics question bank will help to improve subject understanding which will help to get better rank in exams

Frequently Asked Questions by Class 9 Mathematics students

At https://www.cbsencertsolutions.com, we have provided the biggest database of free assignments for Mathematics Class 9 which you can download in Pdf

We provide here Standard 9 Mathematics chapter-wise assignments which can be easily downloaded in Pdf format for free.

You can click on the links above and get assignments for Mathematics in Grade 9, all topic-wise question banks with solutions have been provided here. You can click on the links to download in Pdf.

We have provided here topic-wise Mathematics Grade 9 question banks, revision notes and questions for all difficult topics, and other study material.

We have provided the best collection of question bank and practice tests for Class 9 for all subjects. You can download them all and use them offline without the internet.

Related Posts

Class 9 Mathematics Circle Assignments

Class 9 Mathematics Polynomials Assignments

Class 9 Science Assignments

• Maths Notes Class 9
• NCERT Solutions Class 9
• RD Sharma Solutions Class 9
• Maths Formulas Class 9
• Class 9 Syllabus
• Class 9 Revision Notes
• Physics Notes Class 9
• Chemistry Notes Class 9
• Biology Notes Class 9
• History Notes class 9
• Geography Notes class 9
• Social science Notes class 9

NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables

Chapter 4 of the Class 9 NCERT Mathematics textbook, “Linear Equations in Two Variables,” introduces students to the concept of linear equations involving two variables. This chapter explores the graphical representation of these equations, methods to find solutions, and the relationship between the algebraic and geometric representations. Students will learn to solve linear equations, understand their solutions, and apply these concepts to real-life situations.

NCERT Solutions for Class 9 – Mathematics – Chapter 4 Linear Equations in Two Variables

This section provides detailed solutions to the problems in Chapter 4, “Linear Equations in Two Variables,” from the Class 9 NCERT Mathematics textbook. The solutions help students understand the methods of solving linear equations graphically and algebraically and interpreting the results.

NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables is created by a team of professionals in the field of academic content, to help students resolve their doubts in solving problems given in the NCERT textbook. Use the expert-crafted Class 9 Mathematics Chapter 4 Linear Equations in Two Variables NCERT Answers to gain insights into the context and effective problem-solving approaches for this chapter. Find accurate solutions to all the exercise questions effortlessly. All of the problems in this chapter’s exercise from the NCERT textbook are covered in the NCERT Solutions for Class 9 Maths.

This chapter Linear Equations in Two Variables covers the introduction to linear equations , graphical representation of linear equations , techniques to solve them, formulating equations from real-life situations, and solving word problems. Students learn how to manipulate and solve linear equations in one variable using techniques such as simplification, isolation of the variable, and applying inverse operations.

Exercises under NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables

Ncert solutions for class 9 maths chapter 4 linear equations in two variables: exercise 4.1, question 1. the cost of a notebook is twice the cost of a pen. write a linear equation in two variables to represent this statement..

Let’s take the cost of a notebook as Rs. x and the cost of a pen as Rs. y. Given that cost of a notebook (x) is twice the cost of a pen(y).  So, x = 2y. x – 2y = 0 x – 2y = 0 is the linear equation in two variables that represent the statement.

Question 2. Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case: 

(i) 2x + 3y = 9.35 

2x + 3y – 9.35 = 0 (Transposing 9.35 to LHS) (2)x + (3)y + (-9.35) = 0 (converting it in the form ax + by + c = 0) On comparing equation with ax + by + c = 0,  We get a = 2, b = 3, c = -9.35

(ii) x – y/5 -10 = 0

(5x – y – 50)/5 = 0 (Multiply and divide the whole equation by 5) 5x – y – 50 = 0 (5)x + (-1)y + (-50) = 0 (converting it in the form ax + by + c = 0) On comparing equation with ax + by +c =0,  We get a = 5, b = -1, c = -50

(iii) -2x + 3y = 6

-2x + 3y – 6 = 0 (Transposing 6 to LHS) (-2)x + (3)y+ (-6) = 0 (converting it in the form ax + by + c = 0) On comparing equation with ax + by +c =0,  We get a = -2, b = 3, c = -6

(iv) x = 3y

x – 3y = 0 (Transposing 3y to LHS) (1)x + (-3)y + 0 = 0 (converting it in the form ax + by + c = 0) On comparing equation with ax + by + c = 0,  We get a = 1, b = -3, c = 0

(v) 2x = -5y

2x + 5y = 0 (Transposing 5y to LHS) (2)x + (5)y + 0 = 0 (converting it in the form ax + by + c = 0) On comparing equation with ax + by +c =0,  We get a = 2, b = 5, c = 0

(vi) x + 2 = 0

(1)x + (0)y + 2 = 0 (converting it in the form ax + by + c = 0) On comparing equation with ax + by +c =0,  We get a = 1, b = 0, c = 2

(vii) y – 2 = 0

(0)x + (1)y + (-2) = 0 (converting it in the form ax + by + c = 0) On comparing equation with ax + by +c =0,  We get a = 0, b = 1, c = -2 

(viii) 5 = 2x

5 – 2x = 0 (Transposing 2x to LHS) (-2)x + (0)y + 5 = 0 (converting it in the form ax + by + c = 0) On comparing equation with ax + by + c = 0,  We get a = -2, b = 0, c = 5

Linear Equations in Two Variables: Exercise 4.2

Question 1: which one of the following options is true, and why, y = 3x + 5 has, (i) a unique solution, (ii) only two solutions, (iii) infinitely many solutions.

Given linear equation: y = 3x + 5 Let x = 0, Therefore y = 3 × 0 + 5  = 0 + 5 = 5 Hence, (0, 5) is one solution Now, let x = 1, Therefore y = 3 × 1 + 5 = 3 + 5 = 7 Hence, (1, 8) is another solution Now, let y = 0, Therefore 0 = 3x + 5 x = 5/3 Hence, (5/3, 0) is one another solution. This concludes that different values of x and y give the different values of y and x respectively. As there is also no end to the different types of solution for the linear equation in two variables. Therefore, it can have infinitely many solutions. Hence, option “ (iii) infinitely many solutions ” is the correct answer.

Question 2: Write four solutions for each of the following equations:

(i) 2x + y = 7 

(ii) πx + y = 9 

(iii) x = 4y

(i) 2x + y = 7  Given: 2x + y = 7  To find the four solutions we have to substitute different values for x. Let x = 0 Then, 2x+y = 7 (2 × 0) + y = 7 y = 7 Therefore, we get (x, y) = (0, 7) Let x = 1 Then, 2x+y = 7 (2×1)+y = 7 2+y = 7 y = 7-2 y = 5 Therefore, we get (x, y) = (1, 5) Let x = 2 Then, 2x + y = 7 (2×2) + y = 7 4 + y = 7 y = 7 – 4 y = 3 Therefore, we get (x, y) = (2, 3) Let x = 3 Then, 2x + y = 7 (2×3) + y = 7 6 + y = 7 y = 7 – 6 y = 1 Therefore, we get (x, y) = (3, 1) Finally, the four solutions are (0, 7), (1,5), (2,3), (3, 1) (ii) πx + y = 9 Given: πx+y = 9 To find the four solutions we have to substitute different values for x. Let x = 0 Then, πx + y = 9 (π×0) + y = 9 y = 9 Therefore, we get (x, y) = (0, 9) Let x = 1 Then, πx +y = 9 (π×1) + y = 9 π + y = 9 y = 9 – π Therefore, we get (x, y) = (1, 9 – π) Let x = 2 Then, πx +y = 9 (π×2) + y = 9 2π + y = 9 y = 9 – 2π Therefore, we get (x, y) = (1, 9 – 2π) Let x = 3 Then, πx +y = 9 (π×3) + y = 9 3π + y = 9 y = 9 – 3π Therefore, we get (x, y) = (1, 9 – 3π) Finally, the four solutions are (0, 9), (1, 9 – π), (2, 9 – 2π), (3, 9 – 3π) (iii) x = 4y Given: x = 4y To find the four solutions we have to substitute different values for x. Let x = 0 Then, x = 4y 0 = 4y 4y= 0 y = 0/4 y = 0 Therefore, we get (x, y) = (0,0) Let x = 1 Then, x = 4y 1 = 4y 4y = 1 y = 1/4 Therefore, we get (x, y) = (1,1/4) Let x = 2 Then, x = 4y 2 = 4y 4y = 2 y = 2/4 Therefore, we get (x, y) = (2, 1/2) Let x = 3 Then, x = 4y 3 = 4y 4y = 3 y = 3/4 Therefore, we get (x, y) = (2, 3/4) Finally, the four solutions are (0, 0), (1,1/4), (2, 1/2), (2, 3/4)

Question 3: Check which of the following are solutions of the equation x – 2y = 4 and which are not:

(i) (0, 2) 

(ii) (2, 0) 

(iii) (4, 0)

(iv) (√2 , 4√2) 

(i) (0, 2) Given: x – 2y = 4 As, x=0 and y=2 Hence, substituting the values of x and y in the equation, we get, x – 2y = 4 0 – (2×2) = 4 -4 ≠ 4 L.H.S ≠ R.H.S Therefore, (0, 2) is not a solution to the given equation x – 2y = 4. (ii) (2, 0) Given: x – 2y = 4 As, x = 2 and y = 0 Hence, substituting the values of x and y in the equation, we get, x – 2y = 4 2 – (2×0) = 4 2 – 0 = 4 2 ≠ 4 L.H.S ≠ R.H.S Therefore, (2, 0) is not a solution to the given equation x – 2y = 4. (iii) (4, 0) Given: x – 2y = 4 As, x= 4 and y=0 Hence, substituting the values of x and y in the equation, we get, x – 2y = 4 4 – 2×0 = 4 4 – 0 = 4 4 = 4 L.H.S = R.H.S Therefore, (4, 0) is a solution to the given equation x – 2y = 4. (iv) (√2, 4√2) Given: x – 2y = 4 As, x = √2 and y = 4√2 Hence, substituting the values of x and y in the equation, we get, x – 2y = 4 √2 – (2×4√2) = 4 √2 – 8√2 = 4 -7√2 ≠ 4 L.H.S ≠ R.H.S Therefore, (√2, 4√2) is not a solution to the given equation x – 2y = 4. (v) (1, 1) Given: x – 2y = 4 As, x= 1 and y= 1 Hence, substituting the values of x and y in the equation, we get, x – 2y = 4 1 – (2×1) = 4 1 – 2 = 4 -1 ≠ 4 L.H.S ≠ R.H.S Therefore, (1, 1) is not a solution to the given equation x – 2y = 4.

Question 4: Find the value of k, if x = 2, y = 1 is a solution of the equation 2x + 3y = k.

Given: 2x + 3y = k According to the question, x = 2 and y = 1 is solution of the given equation. Hence, substituting the values of x and y in the equation 2x+3y = k, we get, 2x + 3y = k (2×2) + (3×1) = k 4 + 3 = k 7 = k k = 7 Therefore, the value of k is 7.

Linear Equations in Two Variables: Exercise 4.3

Question 1. draw the graph of each of the following linear equations in two variables:.

(i) x + y = 4 

(ii) x – y = 2 

(iii) y = 3x 

(iv) 3 = 2x + y

(i) To draw the graph x+y=4 , we need at least two solutions of the equation.  We can check that when, x = 0, y = 4,  and x = 4, y = 0  are solutions of the given equation. So, we can use the following table to draw the graph: x y 0 4 4 0 (ii) To draw the graph x-y=2 , we need at least two solutions of the equation. We can check that when, x = 0, y = -2, and x = 2, y = 0 are solutions of the given equation. So, we can use the following table to draw the graph: x y 0 -2 2 0 (iii) To draw the graph y=3x , we need at least two solutions of the equation. We can check that when, x = 0, y =0, and x = 1, y = 3 are solutions of the given equation. So, we can use the following table to draw the graph : x y 0 0 1 3 (iv) To draw the graph 3=2x+y , we need at least two solutions of the equation. We can check that when, x = 0, y =3, and x = 1, y = 1 are solutions of the given equation. So, we can use the following table to draw the graph : x y 0 3 1 1

Question 2. Give the equations of two lines passing through (2, 14). How many more such lines are there, and why?

Here, as given point is (2,14) so x=2 and y=14 We can form various equation such as, y-x = 14-2 = 12 x+y = 2+14 =16 2x+y = 4+14 = 18 y-2x = 14-4 = 10 y = 14 x = 2 and many more…….. In fact, there are infinitely many linear equations which are satisfied by the coordinates of the point (2, 14). As it is stated that there can be infinite lines passing through a point. So here, ⟹

Question 3. If the point (3, 4) lies on the graph of the equation 3y = ax + 7, find the value of a.

The given equation is 3y = ax+7 According to the given point (3,4),  x = 3 and y = 4 As this point lie on this graph, then it will satisfy these points. So substituting the values  3y = ax+7 ⟹ (3×4) = (a×3)+7 12 = 3a+7  3a = 12–7 3a = 5 a =  Hence, the value of a =  .

Question 4. The taxi fare in a city is as follows: For the first kilometer, the fare is ₹ 8 and for the subsequent distance it is ₹ 5 per km. Taking the distance covered as x km and total fare as ₹ y, write a linear equation for this information, and draw its graph.

So, as given in the question, we will take  Distance covered as x km  and total fare as ₹ y Fare for the first kilometer = 8 per km Fare after the first 1km = ₹ 5 per km Let x is the total distance, then the distance after one km will be = (x-1)km Hence., Fare after the first km = 5(x-1) So, in equation form we can conclude that,  The total fare = Fare of first km+ fare after the first km y = 8+5(x-1) y = 8+5(x-1) y = 8+5x – 5 y = 5x+3 To draw the graph y=5x+3 , we need at least two solutions of the equation. We can check that when, x = 0, y =3, and x = -1, y = -2 are solutions of the given equation. So, we can use the following table to draw the graph : x y 0 3 -1 -2

Question 5. From the choices given below, choose the equation whose graphs are given in Fig. 4.6 and Fig. 4.7.

For Fig. 4. 6 

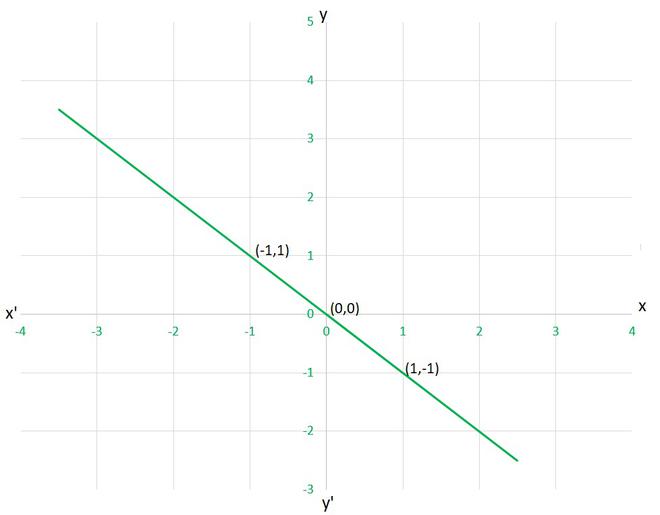
(i) y = x 

(ii) x + y = 0 

(iii) y = 2x 

(iv) 2 + 3y = 7x 

Let’s check each given cases, whether they are satisfying the solution given on graph or not, (i) y=x as given point  (1,-1) x=1 and y=-1 ⟹ x≠y Hence, this equation is INCORRECT for this graph. (ii) x+y=0 as given point (1,-1), (1,-1) and (0,0) x=1 and y=-1 ⟹ x+y=0 x=-1 and y=1 ⟹ x+y=0 x=0 and y=0 ⟹ x+y=0 Hence, this equation is CORRECT for this graph. (iii) y=2x as given point  (1,-1) x=1 and y=-1 ⟹ y≠2x Hence, this equation is INCORRECT for this graph. (iii) 2+3y=7x as given point  (1,-1) x=1 and y=-1 ⟹ 2+3y≠7x Hence, this equation is INCORRECT for this graph.

For Fig. 4.7

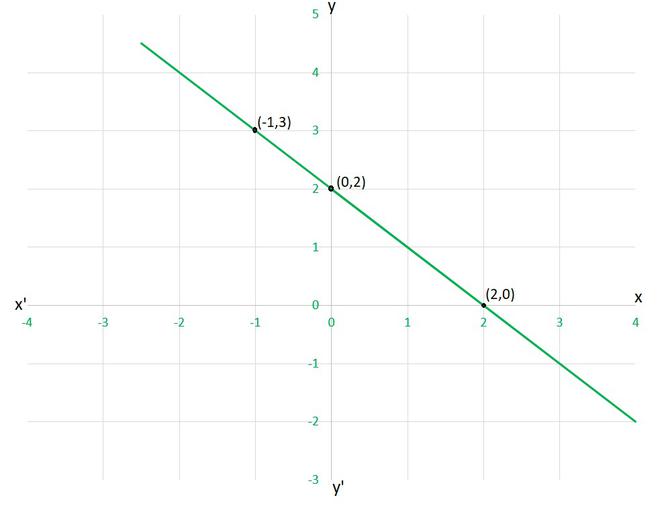
(i) y = x + 2

(ii) y = x – 2

(iii) y = –x + 2

(iv) x + 2y = 6

Let’s check each given cases, whether they are satisfying the solution given on graph or not, (i) y=x+2 as given point (0,2), (2,0) and (-1,3) x=0 and y=2 ⟹ y=x+2 x=2 and y=0 ⟹ y≠x+2 Hence, this equation is INCORRECT for this graph. (ii) y=x-2 as given point (0,2) x=0 and y=2 ⟹ y≠x-2 Hence, this equation is INCORRECT for this graph. (iii) y=-x+2 as given point (0,2) x=0 and y=2 ⟹ y=-x+2 x=2 and y=0 ⟹ y=-x+2 x=-1 and y=3 ⟹ y=-x+2 Hence, this equation is CORRECT for this graph. (iii) x+2y=6 as given point (0,2) x=0 and y=2 ⟹ x+2y≠6 Hence, this equation is INCORRECT for this graph.

Question 6. If the work done by a body on application of a constant force is directly proportional to the distance travelled by the body, express this in the form of an equation in two variables and draw the graph of the same by taking the constant force as 5 units. Also read from the graph the work done when the distance travelled by the body is 

(i) 2 units 

(ii) 0 unit

Given in question, Work done = force × displacement where constant force = 5 units lets take work done as y units and, distance travelled by the body x units Hence, the equation can be expressed as, y=5x To draw the graph y=5x , we need at least two solutions of the equation. We can check that when, x = 0, y =0, and x = 1, y = 5 are solutions of the given equation. So, we can use the following table to draw the graph : x y 0 0 1 5 (i) for x= 2 units y=5×2 work done = 10 units (ii) for x= 0 units y=5×0 work done = 0 units

Question 7. Yamini and Fatima, two students of Class IX of a school, together contributed ₹ 100 towards the Prime Minister’s Relief Fund to help the earthquake victims. Write a linear equation that satisfies this data. (You may take their contributions as ₹ x and ₹ y). Draw the graph of the same. 

Let’s take Yamini’s contribution as ₹ x and Fatima’s contribution as ₹ y. As they together contributed ₹ 100, so the equation can be formed as, x+y=100 To draw the graph x+y=100 , we need at least two solutions of the equation. We can check that when, x = 0, y =100, and x = 100, y = 0 are solutions of the given equation. So, we can use the following table to draw the graph : x y 0 100 100 0

Question 8. In countries like USA and Canada, temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius:

(i) Draw the graph of the linear equation above using Celsius for x-axis and Fahrenheit for y-axis.

(ii) If the temperature is 30°C, what is the temperature in Fahrenheit?

(iii) If the temperature is 95°F, what is the temperature in Celsius?

(iv) If the temperature is 0°C, what is the temperature in Fahrenheit and if the temperature is 0°F, what is the temperature in Celsius?

(v) Is there a temperature which is numerically the same in both Fahrenheit and Celsius? If yes, find it.

(i) Taking Celsius on x-axis and Fahrenheit on y-axis , so equation will be as follows: y =  x + 32 To draw the graph y =  x + 32, we need at least two solutions of the equation. We can check that when, x = 0, y =32, and x = 5, y = 41 are solutions of the given equation. So, we can use the following table to draw the graph : x y 0 32 5 41 (ii) When the temperature is 30°C then, using the equation y =  x + 32 by substituting, x=30, we get y =  ×30 + 32 y = 86  Hence, in Fahrenheit temperature will be 86°F (iii) When the temperature is 95°F then, using the equation y =  x + 32 by substituting, y=95, we get 95 =  x+ 32 x =  x = 35 Hence, in Celsius temperature will be 35°C (iv) When the temperature is 0°C, using the equation y =  x + 32 by substituting, x=0, we get y =  ×0 + 32 y = 32 Hence, in Fahrenheit temperature will be 32°F and, when the temperature is 0°F, using the equation and by substituting, y=0, we get 0 =  x + 32 x =  x = -17.78 Hence, in Celsius temperature will be -17.78°C. (v) Lets take both temperature same as x. so, equation becomes as follows: x =  x + 32 x-x = -32 x = -32 x = -32× x = -40 Hence, Celsius and Fahrenheit temperature will be -40°C and -40°F respectively.

Linear Equations in Two Variables: Exercise 4.4

Question 1. give the geometric representations of y = 3 as an equation.

(i) in one variable

(ii) in two variables

(i) If y = 3 is treated as a equation in one variable y only, then it has the unique solution y = 3, which is a point on the number line (ii) When an equation in two variables, it can be expressed as, 0.x + y – 3 = 0 which is a linear equation in the variables x and y. This is represented by a line. Now all the values of x are permissible because 0.x is always 0. However, y must satisfy the equation y = 3 This has infinitely many solutions . In fact, they are all of the form (r, 3), where r is any real number, so We can have these two solutions for making line on a graph as: x y 0 3 3 3

Question 2. Give the geometric representations of 2x + 9 = 0 as an equation

Firstly, we solve 2x + 9 = 0, to get x = -9/2 (i) If x = -9/2 is treated as a equation in one variable x only, then it has the unique solution x = -9/2, which is a point on the number line. (ii) When an equation in two variables, it can be expressed as, x + 0.y + 9/2 = 0 which is a linear equation in the variables x and y. This is represented by a line. Now all the values of y are permissible because 0.y is always 0. However, x must satisfy the equation x = -9/2 This has infinitely many solutions . In fact, they are all of the form (-9/2, r), where r is any real number, so We can have these two solutions for making line on a graph as: x y -9/2 0 -9/2 5

Types Of Questions In NCERT Class 9 Chapter 4

NCERT Grade 9 CBSE Chapter 4 Linear Equations in Two Variables, falls under the Algebra section. It introduces the concept of solving linear equations with two variables and their graphical representation on a Cartesian plane. The chapter covers essential considerations for solving linear problems and provides solutions for linear equations with two variables. Guided examples make learning more engaging, and exercises help assess understanding. Topics include graphing linear equations, lines parallel to the x-axis and y-axis, and solutions are presented step by step for gradual comprehension.

Benefits of Class 9 Maths Chapter 4 Linear Equations in Two Variables NCERT Solutions

Access all exercise question answers in one convenient location. Gain insights into expertly solved solutions, available for download or online access, to enhance your effectiveness in tackling exercises. Utilize these solutions to hone your problem-solving abilities and grasp the mathematical principles applicable to linear equations with two variables.

Independently resolve doubts associated with exercise questions, ensuring no query goes unanswered and elevating your preparation. Learn from experts’ unique problem-solving approaches for specific questions and apply these insights confidently.

Chapter 4 of the Class 9 NCERT Mathematics textbook, titled “Linear Equations in Two Variables,” introduces students to the concept of linear equations with two variables and their graphical representation. The chapter covers how to solve these equations both algebraically and graphically, and how to interpret their solutions. Students learn to find the relationship between the algebraic expressions and their corresponding graphical representations. This chapter lays the foundation for understanding more complex systems of equations in higher classes.

Related Articles:

• NCERT Solutions for Class 9 English
• NCERT Solutions for Class 9 Biology
• NCERT Solutions for Class 8 to 12
• NCERT Solutions for Class 9 Maths Chapter 10 Circles
• NCERT Solutions for Class 9 Maths Chapter 7 Triangles

FAQs – NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations In Two Variables

What can i learn from maths class 9 chapter 4.

This chapter extends the understanding of linear equations from one variable to two variables. Any equation that can be expressed in the form ax + by + c = 0, where a, b, and c are real numbers, and both ‘a’ and ‘b’ are not zero, is defined as a linear equation in two variables. The NCERT solutions for Class 9 Maths offer chapter-wise answers to exercises in the textbook, allowing students to grasp the concept of linear equations in Algebra through straightforward examples.

What are all the important topics that need to be covered to score in Class 9 Maths Chapter 4?

Key topics essential for a thorough understanding of Class 9 Maths Chapter 4, ‘Linear Equations in Two Variables,’ include expressing linear equations in the form Ax + By + C = 0, exploring various solutions of linear equations with two variables, graphing linear equations in two variables, and understanding equations of lines parallel to the x-axis and y-axis. To gain clarity on these concepts, it’s crucial to solve all examples and exercise questions.

Is Chapter 4 of Linear Equation in Two Variables of Class 9 Maths tough?

No, the NCERT Class 9 Mathematics Chapter 4 Linear Equations in Two Variables, isn’t challenging for those who diligently practice the chapter. The key is to complete the chapter comprehensively, including all examples, exercise questions, and additional problems. To navigate Class 9 Maths Chapter 4 with ease, NCERT Solutions Class 9 Maths Chapter 4 on Linear Equations in Two Variables by GeeksforGeeks is your ideal resource.

Similar Reads

• Mathematics
• School Learning
• Chapterwise-Solutions-Class-9
• Maths-Class-9
• NCERT Solutions Class-9

Please Login to comment...

Improve your coding skills with practice.

What kind of Experience do you want to share?