geometry assignment find the area of each sector

Sector Area Calculator

Table of contents

With this sector area calculator, you'll quickly find any circle sector area , e.g., the area of a semicircle or quadrant. In this short article, we'll:

Provide a sector definition and explain what a sector of a circle is.

Show the sector area formula and explain how to derive the equation yourself without much effort.

Reveal some real-life examples where the sector area calculator may come in handy.

What is a sector of a circle? Sector definition

So let's start with the sector definition – what is a sector in geometry?

A sector is a geometric figure bounded by two radii and the included arc of a circle .

Sectors of a circle are most commonly visualized in pie charts, where a circle is divided into several sectors to show the weightage of each segment. The pictures below show a few examples of circle sectors – it doesn't necessarily mean that they will look like a pie slice, but sometimes it looks like the rest of the pie after you've taken a slice:

You may, very rarely, hear about the sector of an ellipse, but the formulas are way , way more difficult to use than the circle sector area equations.

🙋 Before you continue reading, you should already be familiarized with circles and ellipses. Read our circle calc: find c, d, a, r and our ellipse calculator to ensure you have a firm grasp of these subjects.

Sector area formula

The formula for sector area is simple – multiply the central angle by the radius squared, and divide by 2:

• Sector Area = r² × α / 2

But where does it come from? You can find it by using proportions. All you need to remember is the circle area formula (and we bet you do!):

The area of a circle is calculated as A = πr² . This is a great starting point.

The full angle is 2π in radians, or 360° in degrees, the latter of which is the more common angle unit.

Then, we want to calculate the area of a part of a circle, expressed by the central angle.

For angles of 2π (full circle), the area is equal to πr²:

So, what's the area for the sector of a circle:

α → Sector Area

From the proportion, we can easily find the final sector area formula:

Sector Area = α × πr² / 2π = α × r² / 2

The same method may be used to find arc length – all you need to remember is the formula for a circle's circumference. Read more about this in our circumference calculator and arc length calculator .

💡 Note that α should be in radians when using the given formula. If you know your sector's central angle in degrees , multiply it first by π/180° to find its equivalent value in radians. Or you can use this formula instead, where θ is the central angle in degrees :

Sector Area = r² × θ × π / 360

Special cases: area of semicircle, area of quadrant

Finding the area of a semicircle or quadrant should be a piece of cake now. Just think about what part of a circle they are!

1. Semicircle area: πr² / 2

Knowing that it's half of the circle, divide the area by 2:

Semicircle area = Circle area / 2 = πr² / 2

Of course, you'll get the same result when using the sector area formula. Just remember that the straight angle is π (180°):

Semicircle area = α × r² / 2 = πr² / 2

2. Quadrant area: πr² / 4

As a quadrant is a quarter of a circle, we can write the formula as:

Quadrant area = Circle area / 4 = πr² / 4

Quadrant's central angle is a right angle (π/2 or 90°), so you'll quickly come to the same equation:

Quadrant area = α × r² / 2 = πr² / 4

Sector area calculator – when it may be useful?

We know, we know: " why do we need to learn that? We're never ever gonna use it ". Well, we'd like to show you that geometry is all around us:

If you're wondering how big cake you should order for your awesome birthday party – bingo, that's it! Use the sector area formula to estimate the size of a slice 🍰 for your guests so that nobody will starve to death.

It's a similar story with pizza – have you noticed that every slice is a sector of a circle 🍕? For example, if you're not a big fan of the crust, you can calculate which pizza size will give you the best deal.

Any sewing enthusiasts here?👗 Sector area calculations may be useful in preparing a circle skirt (as it's not always a full circle but, you know, a sector of a circle instead).

Apart from those simple, real-life examples, the sector area formula may be handy in geometry, e.g., for finding the surface area of a cone .

What is the sector of a circle?

The sector of a circle is a slice of a circle, bound by two radiuses and an arc of the circumference . We identify sectors of a circle using their central angle . The central angle is the angle between the two radiuses. Sectors with a central angle equal to 90° are called quadrants .

How do I calculate the area of the sector of a circle?

To calculate the area of the sector of a circle, you can use two methods.

If you know the radius and central angle:

Convert the central angle into radians :

α [rad] = α [deg] · π/180°

Multiply the radius squared by the angle in radians.

Divide the result by 2.

If you know the area of the circle and central angle:

Calculate the ratio between the full angle and the central angle .

Multiply the result by the area of the circle.

What is the area of the 90° sector of a circle with r = 1?

The area of a sector with a central angle α = 90° of a circle with radius r = 1 is π/4 . To calculate this result, you can use the following formula:

A = r² · α/2 ,

substituting:

• r = 1 ; and
• α = 90° · π/180° = π/2 .

A = (1² · π/2)/2 = π/4 .

Notice that this is also a quarter of the area of the whole circle.

How do I find the central angle of a sector?

To find the central angle of a sector of a circle, you can invert the formula for its area :

• r — The radius ; and
• α — The central angle in radians .

The formula for α is then:

α = 2 · A/r²

To find the angle in degrees, multiply the result by 180°/π .

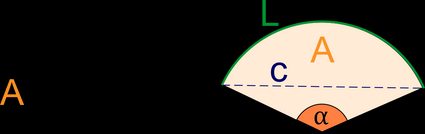
Central angle (⍺)

Diameter (2r)

Sector area (A)

Arc length (L)

Chord length (c)

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

Area Of A Sector

Here we will learn how to calculate the area of a sector including how to identify a sector of a circle, form and use the formula for the area of a sector of a circle and calculate the area of a sector in various scenarios.

There are also area of a sector circle worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is the area of a sector?

The area of a sector is the space inside the section of the circle created by two radii and an arc. It is a fraction of the area of the entire circle.

Major sector : a major sector has a central angle which is more than 180° . Minor sector : a minor sector has a central angle which is less than 180° .

Area of a sector =\frac{\theta}{360} \times \pi r^{2}

θ = angle of the sector

r = radius of the circle

How to find the area of a sector

In order to find the area of a sector you need to be able to find the area of a circle. This is because the area of a sector is part of the total area of the circle.

‘How much’ of the circle is decided by the angle created by the two radii.

The sum of the angle around a point is equal to 360° .

Therefore, the area of a sector is the fraction of the full circle’s area.

The angle is out of 360 or \frac{\theta}{360} , where θ represents the angle, so we can multiply this by the area of the circle to calculate the area of a sector.

NOTE: At GCSE, all angles are measured in degrees. Make sure that your calculator has a small ‘d’ for degrees at the top of the screen rather than an ‘r’ for radians – these are not used until A Level.

Area of a sector formula:

Area of a sector = \frac{\theta}{360} \times \pi r^{2}

In order to solve problems involving the area of a sector you should follow the below steps:

• Find the length of the radius \pmb{r} .
• Find the size of the angle creating the sector.
• Substitute the value of the radius and the angle into the formula for the area of a sector.

Clearly state your answer .

Area of a sector worksheet

Get your free area of a sector worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Related lessons on circles, sectors and arcs

Area of a sector is part of our series of lessons to support revision on sector of a circle and circles, sectors and arcs . You may find it helpful to start with the main circles, sectors and arcs lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• Circles, sectors and arcs
• Sector of a circle
• Perimeter of a sector
• Arc of a circle
• Parts of a circle

Area of a sector examples

Example 1: calculate the area of a sector (quadrant).

Calculate the area of the segment shown below. Give your answer to 3 decimal places.

• Find the length of the radius.

Radius = 6cm .

2 Find the size of the angle creating the sector.

Angle = 90° (shown by the symbol of the right angle).

3 Substitute the value of the radius and the angle into the formula for the area of a sector.

4 Clearly state your answer

The question asked you to round your answer to 3 decimal places

Area of a sector = {9\pi}cm^2

= 28.274333…cm^2

= 28.274cm^2 (3 d.p.)

Example 2: calculate the area of a sector (semicircle)

Calculate the area of the semicircle shown below. Give your answer in terms of \pi.

Find the length of the radius .

Diameter = 24cm

Radius = 12cm – as the radius is half the diameter

Find the size of the angle creating the sector

Angle = 180° . This is because the shape shown is a semicircle. Therefore, the angle of the straight line is 180 degrees.

Substitute the value of the radius, the angle into the formula for the area of a sector .

Area of a sector= \frac{\theta}{360} \times \pi r^{2}

= \frac{180}{360} \times \pi \times 12^{2}

Clearly state your answer

The question asked you to round your answer in terms of \pi :

Area of a sector = 72\pi cm^{2}

Example 3: calculate the area of a sector (with an angle given)

Calculate the area of the sector shown below. Give your answer to 3 significant figures.

Radius = 8cm

Find the size of the angle creating the sector .

Angle = 115°

= \frac{180}{360} \times \pi\times 8^{2}

= \frac{184}{9}\pi

The question asked you to round your answer to 3 significant figures.

Area of a sector = \frac{184}{9}\pi cm^{2}

= 62.228…cm^{2}

= 62.2cm^{2} (3 s.f.)

Example 4: calculate the area of a sector (the angle is not given)

Calculate the area of the sector AOB below.

The length of the radius (OB) is 9cm

The length of a chord (AB) is 10cm .

Give your answer to 2 decimal places

Find the length of the radius

Radius = 9cm

In this example you are not given the angle of the sector, you need to calculate it first.

Here you can use the triangle created by the two radii and the chord to find the angle (see below)

In this example you need to apply the cosine rule to find the angle. 

a^2=b^2+c^2-2bcCos(A)

A is the angle you are trying to find. You can therefore use the rearranged cosine rule to find the angle.

The size of the angle creating the sector (made by the two radii) is 67.498° .

Substitute the value of the radius, the angle into the formula for the area of a sector. 

= \frac{67.498}{360} \times \pi\times 9^{2}

= 47.71152…

Notice in this example how your calculator does not automatically give your answer in terms of pi.

The question asked you to round your answer to 2 decimal places

Area of a sector = 47.71152… cm^{2}

= 47.71 cm^{2} (2 d.p.)

How to solve problems involving an area of a sector

Sometimes you may be given the area of the sector and asked to find a property of the circle such as the radius. In this case you need to ‘reverse’ the process.

• Clearly state which of the properties you know and do not know (e.g. radius, angle of sector, area of sector).
• Using the formula for the area of a sector create an equation and solve for the unknown property you have been asked to find.
• Clearly state your answer (check how the questions asks for the answers to be rounded).

Solving problems involving an area of a sector examples

Example 5: finding the radius given the area of the sector.

The sector below has an area of 20cm^2 . Calculate the length of x . Give you answer to 2 decimal places

Clearly state which of the properties you know and do not know (e.g. radius, angle of sector, area of sector) .

Angle of sector = 115°

Area of sector = 20cm^2

Using the formula for the area of a sector create an equation and solve for the unknown property you have been asked to find .

Clearly state your answer (check how the questions asks for the answers to be rounded) .

The question asks you to give your answer to 2 decimal places

Example 6: finding the angle of a sector given the area of the sector

The sector below has an area of 62cm^2 . Calculate the length of x . Give you answer to 2 decimal places

Radius = 8.5

Angle of sector = x°

Area of sector = 62cm^2

The question asks you to give your answer to 2 decimal places:

Common misconceptions

• Confusing the segment/sector

A segment is made from a chord whilst a sector will have lines (radii) coming from the origin. 

Sectors are a portion of a circle – it can be helpful to think of a sector as a pizza slice.

• Finding the area of the whole circle not the area of the sector

Remember to find the fraction of the circle that makes the sector not just the area of the whole circle.

\frac{\theta}{360} \times \pi r^{2}

To find the area of a sector

• Incorrect use of the cosine rule

Many mistakes are made when applying other rules within a sector question, such as the cosine rule. Take your time with these parts and regularly ask if your answer makes sense within the context of the question. If you need to review the cosine rule do so before continuing on further. 

Practice area of a sector questions

1. What is the angle of the sector for a quadrant?

A quadrant is a quarter of a circle. Angles around a point are equal to 360^{\circ} so a quadrant will be a quarter of 360^{\circ} .   360\div4 =90  

2. What is the angle of the sector for a semi-circle?

A semi circle is half a circle. Angles around a point are equal to 360^{\circ} so a half will be half of 360^{\circ} .   360\div2 =180  

Area of a sector = \frac{\theta}{360} \times \pi r^{2}   \frac{90}{360} \times \pi\times 10^{2} =25\pi  

Area of a sector = \frac{\theta}{360} \times \pi r^{2}   \frac{180}{360} \times \pi\times 10^{2 }= 50\pi  

Area of a sector = \frac{\theta}{360} \times \pi r^{2}   \frac{270}{360} \times \pi\times 8^{2} = 48\pi

Area of a sector = \frac{\theta}{360} \times \pi r^{2}   \frac{315}{360} \times \pi\times 8^{2} = 56\pi

Area of a sector GCSE questions

1. The diagram shows a sector of a circle with centre O .   The radius of the circle is 13cm . The angle of the sector is 150^{\circ}.  

Calculate the area of the sector, give your answer correct to 3 significant figures.

\frac{150}{360}\times \pi \times 13^2

\frac{290}{360}\times \pi \times 6.5^2

106.923…

Calculate the area of the sector, give your answer correct to 2 decimal places.

\frac{60}{360}\times \pi \times 4.9^2

12.57 cm^{2}

5\pi=\frac{x}{360} \times \pi \times 10^2   Correct attempt to form an equation for the area of the sector

Attempt to solve equation for x , with two steps completed correctly

30=\frac{135}{360} \times \pi \times x^2   Correct attempt to form an equation for the area of the sector

\frac{80}{\pi} or 25.46479… seen

5.04626 negative solution cannot be the solution

Learning checklist

You have now learned how to:

• Identify and apply circle definitions and properties, including: centre, radius, chord, diameter, circumference
• Identify and apply circle definitions and properties, including tangent, arc, sector and segment
• Calculate areas of a sector
• Calculate a property of a circle given the area of its sector

The next lessons are

• How to work out perimeter
• Angle rules
• Angles in polygons

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.3: Area of a Sector

• Last updated
• Save as PDF
• Page ID 35459

• Michael Corral
• Schoolcraft College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

In geometry you learned that the area of a circle of radius \(r \) is \(\pi r^2 \). We will now learn how to find the area of a sector of a circle. A sector is the region bounded by a central angle and its intercepted arc, such as the shaded region in Figure 4.3.1.

Let \(\theta \) be a central angle in a circle of radius \(r \) and let \(A \) be the area of its sector. Similar to arc length, the ratio of \(A \) to the area of the entire circle is the same as the ratio of \(\theta \) to one revolution. In other words, again using radian measure,

\[ \frac{\text{area of sector}}{\text{area of entire circle}} ~=~ \frac{\text{sector angle}}{\text{one revolution}} \quad\Rightarrow\quad \frac{A}{\pi\,r^2} ~=~ \frac{\theta}{2\pi} ~. \nonumber \]

Solving for \(A \) in the above equation, we get the following formula:

In a circle of radius \(r \), the area \(A \) of the sector inside a central angle \(\theta \) is

\[ A ~=~ \tfrac{1}{2}\,r^2 \;\theta ~,\label{eqn:sectorarea} \]

where \(\theta \) is measured in radians.

Example 4.8

Find the area of a sector whose angle is \(\frac{\pi}{5} \) rad in a circle of radius \(4\) cm.

Using \(\theta=\frac{\pi}{5} \) and \(r=4 \) in Equation \ref{eqn:sectorarea}, the area \(A \) of the sector is

\[ A ~=~ \tfrac{1}{2}\,r^2 \;\theta ~= \tfrac{1}{2}\,(4)^2 \;\cdot\;\tfrac{\pi}{5} ~=~ \boxed{\tfrac{8\pi}{5}~\text{cm}^2} ~. \nonumber \]

Example 4.9

Find the area of a sector whose angle is \(117^\circ \) in a circle of radius \(3.5 \) m. Solution:

As with arc length, we have to make sure that the angle is measured in radians or else the answer will be way off. So converting \(\theta=117^\circ \) to radians and using \(r=3.5 \) in Equation \ref{eqn:sectorarea} for the area \(A \) of the sector, we get

\[ \theta ~=~ 117^\circ ~=~ \frac{\pi}{180} \;\cdot\; 117 ~=~ 2.042~\text{rad} \quad\Rightarrow\quad A ~=~ \tfrac{1}{2}\,r^2 \;\theta ~= \tfrac{1}{2}\,(3.5)^2 \;(2.042) ~=~ \boxed{12.51~\text{m}^2} ~. \nonumber \]

For a sector whose angle is \(\theta \) in a circle of radius \(r \), the length of the arc cut off by that angle is \(s=r\,\theta \). Thus, by Equation \ref{eqn:sectorarea} the area \(A \) of the sector can be written as:

\[ \boxed{ A ~=~ \tfrac{1}{2}\,rs}\label{eqn:sectorarc} \nonumber \]

Note: The central angle \(\theta \) that intercepts an arc is sometimes called the angle subtended by the arc.

Example 4.10

Find the area of a sector whose arc is \(6 \) cm in a circle of radius \(9 \) cm.

Using \(s=6 \) and \(r=9 \) in Equation \ref{eqn:sectorarc} for the area \(A \), we get

\[ A ~=~ \tfrac{1}{2}\,rs ~=~ ~=~ \tfrac{1}{2}\,(9)\,(6) ~=~ \boxed{27~\text{cm}^2} ~. \nonumber \]

Note that the angle subtended by the arc is \(\theta = \frac{s}{r} = \frac{2}{3} \) rad.

Example 4.11

Find the area \(K \) inside the belt pulley system from Example 4.7 in Section 4.2. Solution:

Recall that the belt pulleys have radii of \(5 \) cm and \(8 \) cm, and their centers are \(15 \) cm apart. We showed in Example 4.7 that \(EF=AC=6\,\sqrt{6} \), \(\angle\,DAE=1.37 \) rad, and \(\angle\,GBF=1.77 \) rad. We see from Figure 4.3.2 that, by symmetry, the total area \(K \) enclosed by the belt is twice the area above the line \(\overline{DG} \), that is,

\[\nonumber \begin{align*} K ~=~ 2\,( (&\text{Area of sector \(DAE\)}) ~+~ (\text{Area of rectangle \(AEFC\)})\\ \nonumber &+~ (\text{Area of triangle \(\triangle\,ABC\)}) ~+~ (\text{Area of sector \(GBF\)}) )~. \end{align*} \nonumber \]

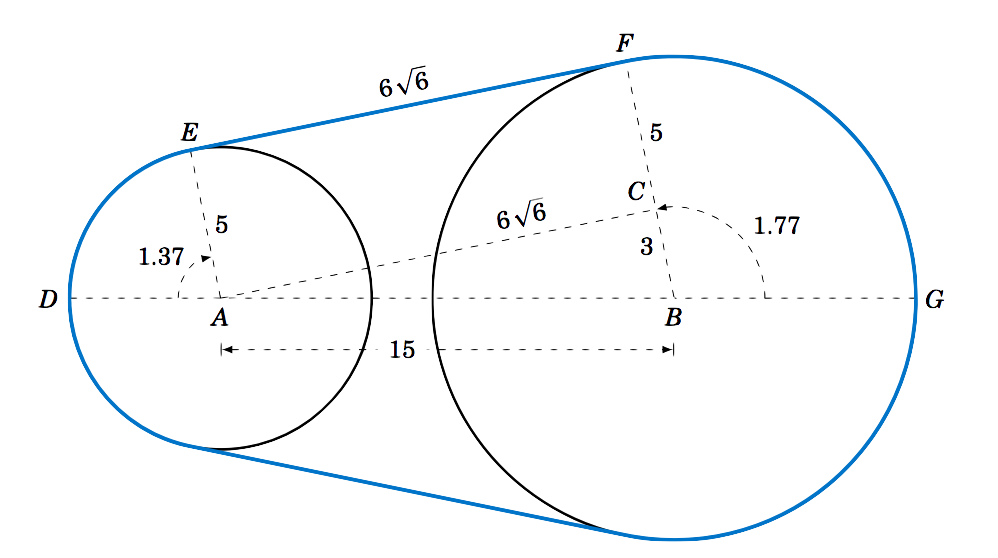
Since \(AEFC \) is a rectangle with sides \(5 \) and \(6\,\sqrt{6} \), its area is \(30\,\sqrt{6} \). And since \(\triangle\,ABC \) is a right triangle whose legs have lengths \(3 \) and \(6\,\sqrt{6} \), its area is \(\frac{1}{2}\,(3)\,(6\,\sqrt{6}) = 9\,\sqrt{6} \). Thus, using Equation \ref{eqn:sectorarea} for the areas of sectors \(DAE \) and \(GBF \), we have

\[\nonumber \begin{align*} K ~&=~ 2\,\left( (\text{Area of sector \(DAE\)}) \;+\; 30\,\sqrt{6} \;+\; 9\,\sqrt{6} \;+\; (\text{Area of sector \(GBF\)}) \right)\\ \nonumber &=~ 2\,\left( \tfrac{1}{2}\,(5)^2 \,(1.37) ~+~ 30\,\sqrt{6} ~+~ 9\,\sqrt{6} ~+~ \tfrac{1}{2}\,(8)^2 \,(1.77) \right)\\ \nonumber &=~ \boxed{338.59~\text{cm}^2}~. \end{align*} \nonumber \]

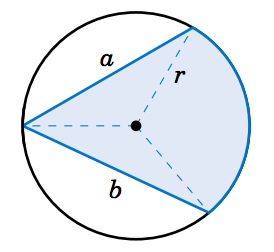
So far we have dealt with the area cut off by a central angle. How would you find the area of a region cut off by an inscribed angle, such as the shaded region in Figure 4.3.3? In this picture, the center of the circle is inside the inscribed angle, and the lengths \(a \) and \(b\) of the two chords are given, as is the radius \(r \) of the circle. Drawing line segments from the center of the circle to the endpoints of the chords indicates how to solve this problem: add up the areas of the two triangles and the sector formed by the central angle. The areas and angles of the two triangles can be determined (since all three sides are known) using methods from Chapter 2. Also, recall (Theorem 2.4 in Section 2.5) that a central angle has twice the measure of any inscribed angle which intercepts the same arc. In the exercises you will be asked to solve problems like this (including the cases where the center of the circle is outside or on the inscribed angle).

Another type of region we can consider is a segment of a circle, which is the region between a chord and the arc it cuts off. In Figure 4.3.4 the segment formed by the chord \(\overline{AB} \) is the shaded region between the arc \(\overparen{AB} \) and the triangle \(\triangle\,OAB \). By Equation 2.23 in Section 2.4 for the area of a triangle given two sides and their included angle, we know that

\[ \text{area of } \triangle\,OAB ~=~ \tfrac{1}{2}\,(r)\,(r)\,\sin\;\theta ~=~ \tfrac{1}{2}\,r^2 \,\sin\;\theta ~. \nonumber \]

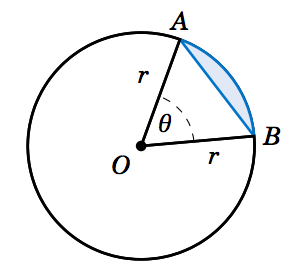
Thus, since the area \(K \) of the segment is the area of the sector \(AOB \) minus the area of the triangle \(\triangle\,OAB \), we have

\[ \text{area \(K \) of segment } AB ~=~ \tfrac{1}{2}\,r^2 \;\theta ~-~ \tfrac{1}{2}\,r^2 \,\sin\;\theta ~=~ \boxed{\tfrac{1}{2}\,r^2 \,(\theta - \sin\;\theta)} ~.\label{eqn:segment} \nonumber \]

Note that as a consequence of Equation \ref{eqn:segment} we must have \(\;\theta > \sin\;\theta\) for \(0 < \theta \le \pi \) (measured in radians), since the area of a segment is positive for those angles.

Example 4.12

Find the area of the segment formed by a chord of length \(3 \) in a circle of radius \(2 \).

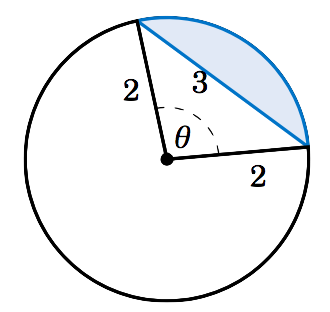
Figure 4.3.5 shows the segment formed by a chord of length \(3 \) in a circle of radius \(r=2 \). We can use the Law of Cosines to find the subtended central angle \(\theta\):

\[ \cos\;\theta ~=~ \frac{2^2 + 2^2 - 3^2}{2\,(2)\,(2)} ~=~ -0.125 \quad\Rightarrow\quad \theta ~=~ 1.696~\text{rad} \nonumber \]

Thus, by Equation \ref{eqn:segment} the area \(K \) of the segment is:

\[ K ~=~ \tfrac{1}{2}\,r^2 \,(\theta - \sin\;\theta) ~=~ \tfrac{1}{2}\,(2)^2 \, (1.696 - \sin\;1.696) ~=~ \boxed{1.408} \nonumber \]

Example 4.13

The centers of two circles are \(7 \) cm apart, with one circle having a radius of \(5 \) cm and the other a radius of \(4 \) cm. Find the area \(K \) of their intersection. Solution:

In Figure 4.3.6(a), we see that the intersection of the two circles is the union of the segments formed by the chord \(\overline{CD} \) in each circle. Thus, once we determine the angles \(\angle\,CAD \) and \(\angle\,CBD \) we can calculate the area of each segment and add those areas together to get \(K \).

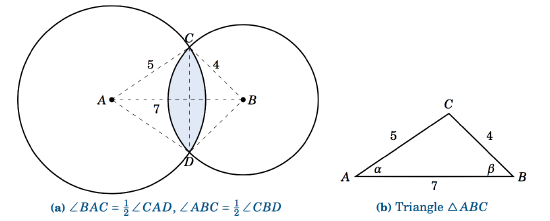
By symmetry, we see that \(\angle\,BAC = \frac{1}{2}\,\angle\,CAD \) and \(\angle\,ABC = \frac{1}{2}\,\angle\,CBD \). So let \(\alpha = \angle\,BAC \) and \(\beta = \angle\,ABC \), as in Figure 4.3.6(b). By the Law of Cosines, we have

\[ \begin{alignat*}{7} \cos\;\alpha ~&=~ \frac{7^2 + 5^2 - 4^2}{2\,(7)\,(5)} ~&=~ 0.8286 \quad&\Rightarrow\quad \alpha ~&=~ 0.594~\text{rad} \quad&\Rightarrow\quad \angle\,CAD ~&=~2\,(0.594) = 1.188~\text{rad}\\ \nonumber \cos\;\beta ~&=~ \frac{7^2 + 4^2 - 5^2}{2\,(7)\,(4)} ~&=~ 0.7143 \quad&\Rightarrow\quad \beta ~&=~ 0.775~\text{rad} \quad&\Rightarrow\quad \angle\,CBD ~&=~ 2\,(0.775) = 1.550~\text{rad} \end{alignat*} \nonumber \]

Thus, the area \(K \) is

\[\nonumber \begin{align*} K ~&=~ (\text{Area of segment \(CD \) in circle at \(A\)}) ~+~ (\text{Area of segment \(CD \) in circle at \(B\)})\\ \nonumber &=~ \tfrac{1}{2}\,(5)^2 \,(1.188 - \sin\;1.188) ~+~ \tfrac{1}{2}\,(4)^2 \,(1.550 - \sin\;1.550)\\ \nonumber &=~ \boxed{7.656~\text{cm}^2} ~. \end{align*} \nonumber \]

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

High school geometry

Course: high school geometry   >   unit 8, area of a sector.

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics
• Calculating Volume and Area

How to Calculate the Area of a Sector

Last Updated: March 11, 2023 Fact Checked

This article was reviewed by Grace Imson, MA . Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 224,995 times.

Sometimes you might need to determine the area of a sector, say for math questions or for a project you are working on. A sector is a part of a circle that is shaped like a piece of pizza or pie. To find the area of this piece, you need to know the radius, arc length and the degree of the central angle. With this information, finding the area of a sector is a simple matter of plugging the numbers into given formulas.

Calculating the Area with a Known Central Angle and Radius

• A circle is 360 degrees, so when you place the measurement of the sector's central angle over 360, it gives you the fraction of the whole circle. [2] X Research source

• For example, if the central angle is 100 degrees, you will divide 100 by 360, to get 0.28. (The area of the sector is about 28 percent of the area of the whole circle.)
• If you don't know the measurement of the central angle, but you know what fraction of the circle the sector is, determine the measurement of the angle by multiplying that fraction by 360. For example, if you know the sector is one-fourth of the circle, multiply 360 by one-fourth (.25) to get 90 degrees.

• For example, if the radius is 5 cm, you will square 5 to get 25, and then multiply 25 by 3.14, to get 78.5.
• If you don't know the length of the radius, but you know the diameter, simply divide the diameter by 2 to find the radius.

• For example, 0.28 x 78.5 = 21.89.
• Since you are finding the area, the answer will be in square centimetres.

Calculating the Area with a Known Arc Length and Radius

• Remember the formula for finding the circumference (perimeter) of a circle is 2𝝅r. If you know the length of the arc (which is a portion of the circumference), you can find what fraction of the circle the sector represents by comparing the arc length to the total circumference.

• For example, if the arc length is 5 cm and the radius is 8 cm, your new numerator will be 40.

• Since you are finding the area, your answer will be in square centimetres.

Community Q&A

You Might Also Like

• ↑ https://www.khanacademy.org/math/geometry-home/geometry-area-perimeter/geometry-perimeter/v/perimeter-and-area-basics
• ↑ https://www.youtube.com/watch?v=cAOVS2DTU0U
• ↑ https://www.youtube.com/watch?v=4BXMGuQdiBo
• ↑ https://www.mathopenref.com/arcsectorarea.html
• ↑ https://www.khanacademy.org/math/geometry/hs-geo-circles/hs-geo-sectors/v/area-of-a-sector-given-a-central-angle

About This Article

To calculate the area of a sector, start by finding the central angle of the sector and dividing it by 360. Next, take the radius, or length of one of the lines, square it, and multiply it by 3.14. Then, multiply the two numbers to get the area of the sector. For example, if the central angle is 100 degrees and the radius is 5, you would divide 100 by 360 to get .28. Then, square 5 to get 25 before multiplying it by 3.14 for an answer of 78.5. Finally, multiply .28 by 78.5 for a final answer of 21.89, which is the area of the sector. To learn how to calculate the area of a sector if you don’t know the central angle, read on! Did this summary help you? Yes No

• Send fan mail to authors

Did this article help you?

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

Don’t miss out! Sign up for

wikiHow’s newsletter

Area of a Circle by Cutting into Sectors

Here is a way to find the formula for the area of a circle:

Cut a circle into equal sectors (12 in this example)

Divide just one of the sectors into two equal parts. We now have thirteen sectors – number them 1 to 13:

Rearrange the 13 sectors like this:

Which resembles a rectangle:

What are the (approximate) height and width of the rectangle?

The height is the circle's radius : just look at sectors 1 and 13 above. When they were in the circle they were "radius" high.

The width (actually one "bumpy" edge) is half of the curved parts around the circle ... in other words it is about half the circumference of the circle.

We know that:

Circumference = 2 × π × radius

And so the width is about:

Half the Circumference = π × radius

And so we have (approximately):

Now we multply width by height to find the area of the rectangle:

Note: The rectangle and the "bumpy edged shape" made by the sectors are not an exact match.

But we can get a better result if we divide the circle into 25 sectors (23 with an angle of 15° and 2 with an angle of 7.5°).

And the more we divide the circle up, the closer we get to being exactly right.

Area of Circle = π r 2